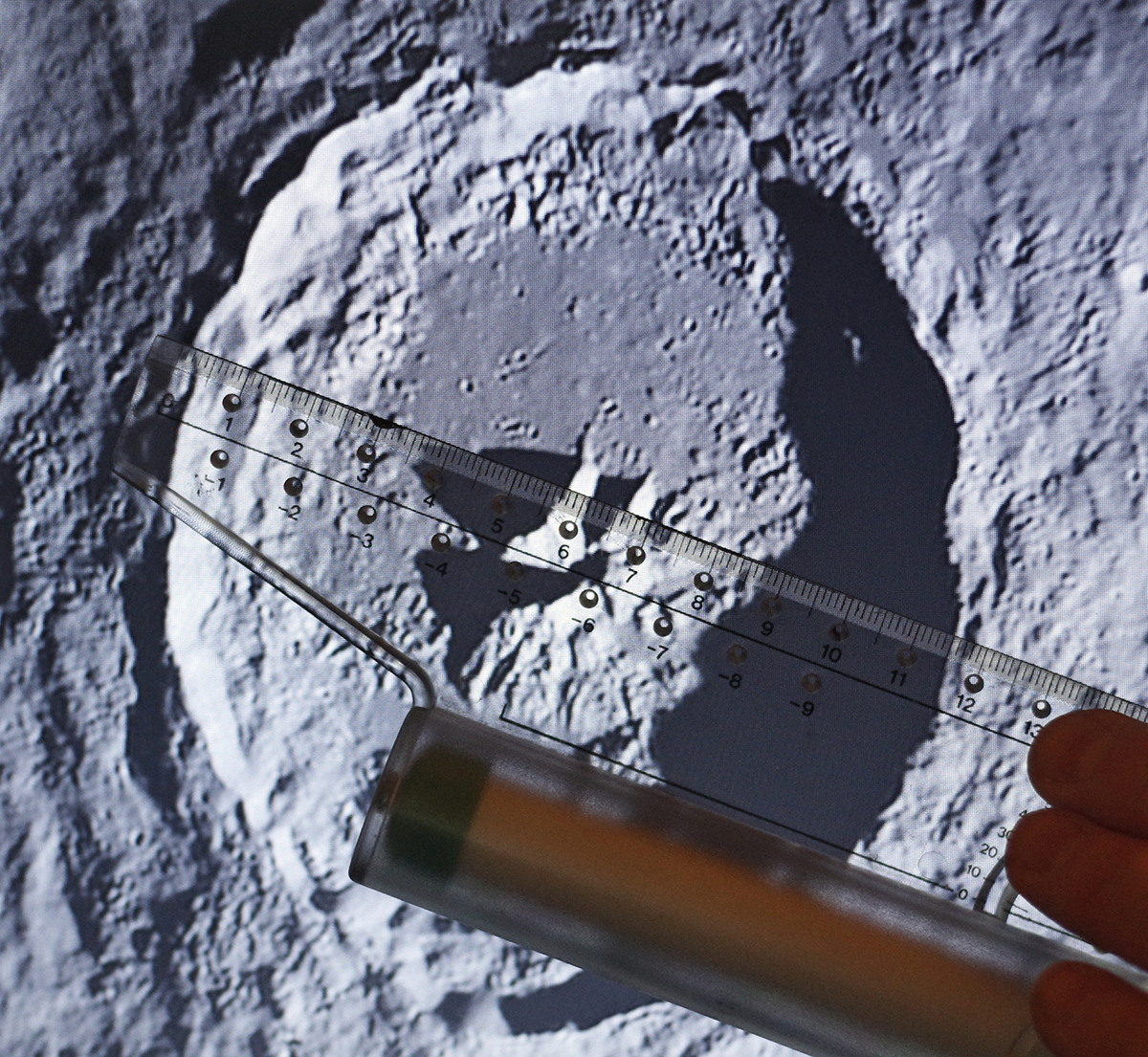
The lunar surface is at its most striking when there are well-defined shadows. As well as being visually pleasing, the study of shadows cast by lunar mountains and craters can tell us a lot about these features.
When we see a lunar crater from above it’s easy to think that the crater wall is uniform around the entire perimeter.
However, if we look at the shape of the shadows cast by a crater wall, we can get a clearer sense of the peaks and troughs along the rim.
For lunar observing advice, read our guide on how to observe the Moon or sign up to receive the BBC Sky at Night Magazine e-newsletter.

If the crater has a central peak its shadows will reveal its nature too.
In this guide we'll show you a straightforward method to measure the shadows in lunar craters.
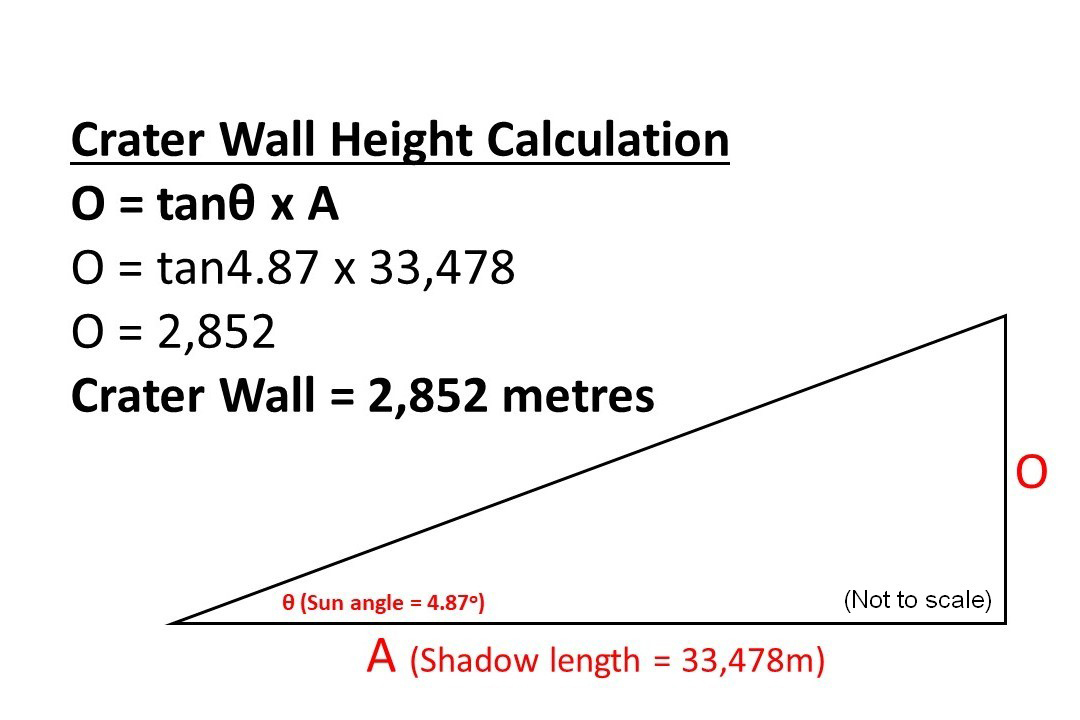
By using some simple right-angled triangle trigonometry we can calculate the height of the lunar feature casting the shadow.
Our equation is:
O = tanθ x A; where O = ‘opposite’ (ie the height of the feature), tanθ = the tangent of the Sun angle, and A = ‘adjacent’ (ie the length of the shadow).
What you need to measure craters on the Moon

To get started all you need is a ruler, a calculator and a photo of a crater that has clear shadows.
You need the time and date the photo was taken, and you can use the Lunar Terminator Visualization Tool to find out what the Sun angle was at that time, at any point on the lunar surface.
We used a photo of crater Theophilus taken by Alessandro Bianconi at 03:48 UT on 18 September 2011.
It is important to mention that our process here has been simplified.
This method relies on a published crater diameter so we can scale up our shadow measurement.
Most craters are not perfectly circular, so the published figure is an average. We only took one diameter measurement.
If you use this calculation for an isolated feature, you’ll need to know the pixel/kilometre ratio for the equipment used to take photo.
Additionally, our process doesn’t take the curvature of the lunar surface into account.
Remember, the Moon is a sphere, so if you chose a crater that is quite central, the foreshortening effects are less apparent.
It can also be difficult to know exactly where the shadow starts and ends if it’s located in a complex region.
We are only using a single measurement of a complex crater at one Sun angle and comparing that to a published figure, which will be an average value.
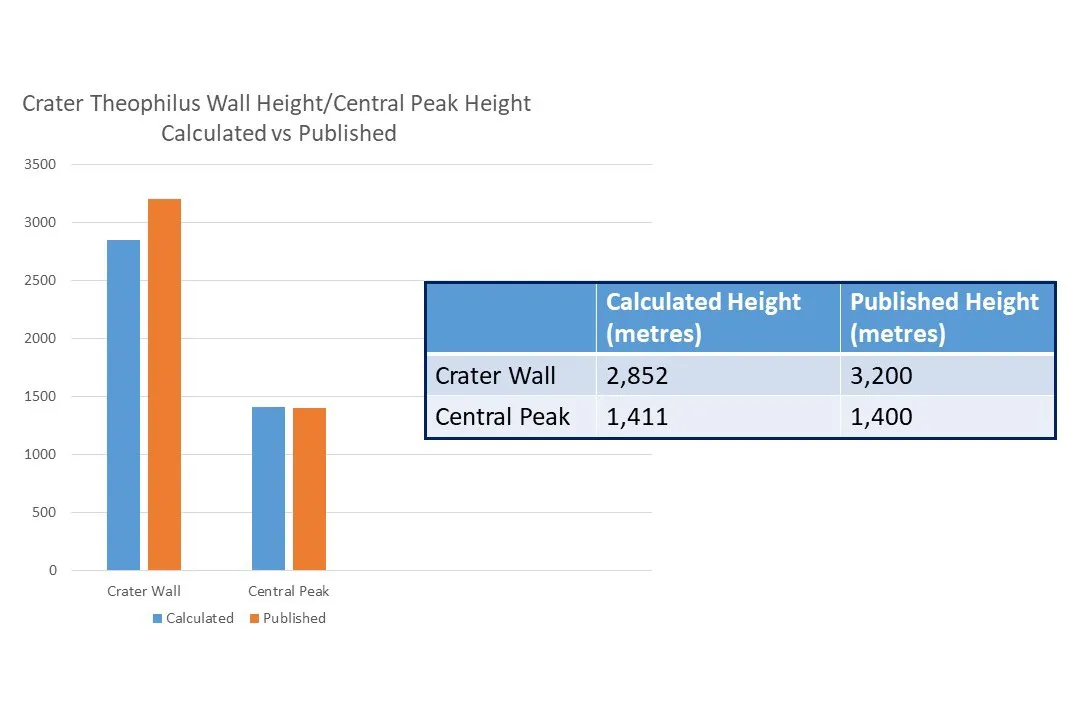
Our method brings a sense of scale to an otherwise abstract landscape. Even though it has been simplified to make the maths easier, it still yields results that are close to the published figure.
This project will help you to gain a deeper awareness of the lunar features you choose to analyse.

You will need
- A high-resolution digital photo of a lunar crater that has clearly defined shadows; we used a photo of the crater Theophilus
- A ruler; we used it to measure the shadow lengths on the computer screen, but you can use Photoshop’s measuring tool or a printed photo
- A scientific calculator with a tan button. If you use Excel for these calculations, convert the Sun angle from degrees to radians first
- A copy of the Lunar Terminator Visualization Tool
- The published crater diameter figure for the crater you’re measuring from this online list of near-side craters.