Ever heard of spacetime? For many of us, learning about this seemingly strange concept muddles what we knew about the physics of space, which we thought were relatively simple.
Like me, you’ve probably had a pretty good grasp of what space is since you were quite young. It’s what I want more of in my telescope room.
It’s also something big, black and sparkly that is usually obscured by clouds.
For a few of my formative years, I was confused by Captain Kirk’s claim that it’s ‘the final frontier’, before coming to the realisation that outer space really is the same stuff as the space inside our homes – just much bigger.
By the time my maths teacher had taught us about the x, y and z coordinates, my appreciation of three-dimensional space seemed to be complete.
It’s three-dimensional because you need three coordinates to specify a particular location (its distance up, forwards and across)... got it!
For more mind-blowing space science read our guides How do we measure distance in space? and What happened during the first seconds of the Universe?

So I was perplexed and intrigued when I heard that things are more complicated: my home is actually full of something called spacetime, which is, apparently, four-dimensional.
Let’s say that this fourth element, time, is represented by the letter t. I have no trouble counting up to four, or with agreeing that x, y, z and t make a total of four coordinates.
But why in the name of sanity would anyone want to group them together and call them spacetime?
It would make as much sense to define the intensity of an odour with the letter p and say that my house is full of ‘spacepong’ (with the coordinates x, y, z and p).
My cooker is in the kitchen, at spacepong coordinates 1, 1, 0, 3.14159... while my socks are festering under the bed at location 2, 0, 4, ∞.
We’ve all heard the assertion of everyone’s favourite wild-haired German that the apparent difference between space and time is some kind of illusion, and they’re really the same stuff.
Yes, I mean Einstein. If you hear it enough times, you come to accept it, but is it sensible?
I thought my son was seven years old and 4ft tall, but maybe he’s 10 miles old and a fortnight tall? Pull the other one!
Time really is altogether different from space, right? I’m here to say ‘yes!’ ...and ‘no’. Here’s how it works.
Understanding the dimensions of space
First, we need to understand what makes normal space three-dimensional. What distinguishes the x, y and z coordinates of space from any other set of three unrelated measurements like the height, weight and odour of my socks?
The crucial thing is that the three space coordinates can get mixed up with each other, so that different observers can disagree about their values.
With that idea in mind, allowing us to distinguish coordinates belonging to the same space from a collection of independent measurements, let’s return to Einstein’s idea that space and time are really part of the same four-dimensional thing.
"So Albert, are you suggesting that two people, observing the same scene from different points of view, could mix up their respective measurements of the position and time of something they see, and so end up disagreeing about how long it took?"
Einstein: "Ja!"
That is exactly what happens in Einstein’s famous ‘thought experiment’, where he imagined a pair of twins getting into two rockets and simultaneously zooming off at fantastically high speeds in opposite directions.
The hirsute clever-clogs had an inkling that something fishy was happening to time, having heard about some recent experiments involving the speed of light, carried out by a pair of scientists called Michelson and Morley.
So in his thought experiment, he added a make-believe, ultra-reliable clock to each of the rockets.
Each clock consisted of two parallel mirrors with a short burst of light trapped between them. The light bounces back and forth, making the clock tick or tock each time it is reflected.
This clock design should be super-accurate because the speed of light never varies. It’s always 299,792,458m/s, and I mean always.

The peculiar experimental findings of Michelson and Morley showed that, no matter whether you are standing still, or moving fast in the same direction as the light, you still see it travelling at 299,792,458m/s relative to you.
This seems very strange. If I’m driving at 30 miles per hour past a cinema and I’m overtaken by an SUV doing 75 miles per hour relative to the cinema, then I see it going past at 45 miles per hour relative to me.
This common everyday experience is at odds with the experiment on light, which showed that its speed is always the same relative to you, no matter how fast you’re going.
So, Einstein fits each rocket with an utterly dependable light-clock, and lets the experiment unfold.
Come and ride with one of the twins – let’s call him Castor.
Sitting comfortably in his rocket’s leather-upholstered drawing room, you hear the frantic ticking of his light clock as it stands stationary (relative to you) on the floor, keeping perfect time.
Glancing through the rocket’s mock-Tudor bay window, you observe Castor’s brother Pollux passing by at incredibly high speed and notice that the light trapped in his clock must take a zig-zagging path in order to keep up with the moving rocket.
Pollux’s light has to travel farther between tick and tock than the light in your static clock. Of course, you observe the light inside Pollux’s clock moving at 299,792,458m/s, just the same as your own clock’s light so, since it has farther to go, it takes longer to cross his clock; longer to tick-tock.
Pollux’s clock is running slow! His clock is made of radiation passing through space and that is more or less the design of every atom in his body too.
So everything is running slow over there on brother Pollux’s spaceship. He’s even ageing more slowly than Castor.
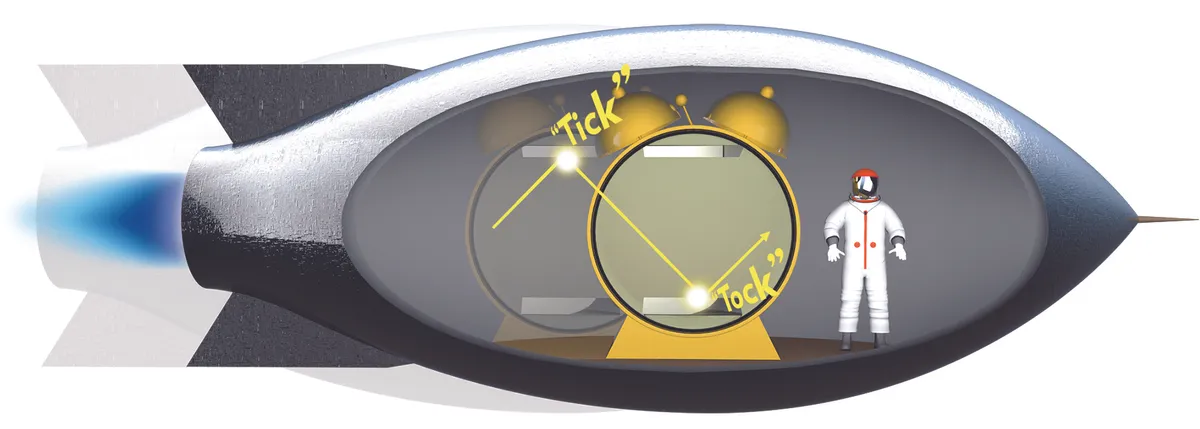
The twin paradox
So far, so bizarre, but here comes the really weird bit. If you had hitched a lift with Pollux instead of his twin, you would have believed that his clock was stationary (relative to you) and Castor’s rocket and clock were zooming past, and therefore ticking more slowly.
Pollux’s clock runs slower than Castor’s and Castor’s clock runs slower than Pollux’s. This is Einstein’s famous ‘twin paradox’.
Finding a paradox usually indicates that there is a mistake somewhere in our reasoning, but not in this case. Both of these conflicting statements are true.
How long something takes to happen depends on your point of view.
And remember, that’s exactly the telltale sign we were looking for – the clue that time is really just one coordinate of a higher-dimensional space-type thing.
Two observers can disagree about which thing took longer – the ticking of Castor’s clock or of Pollux’s, depending on which ‘direction’ they are looking from.
So it turns out that the way to ‘rotate’ your time axis, so that it gets mixed up with your x, y and z readings, is to travel very fast!
Incredible though it seems, everything discussed so far – the rockets, the clocks, the rotating of time into space – is not a metaphor: this stuff really happens.
At the relatively low speeds of ordinary terrestrial things, our time directions are not rotated much and our clocks all agree, more or less.
But astronomers have actually seen very fast-moving things ageing slowly. Every day, our planet is bombarded by super-fast cosmic rays, that have a very different point of view regarding distance and time.
The importance of perspective

Let’s draw an analogy to show how two people, in tip-top mental health, could disagree about which of two things is longer.
Two surveyors have been asked to measure two straight roads and find which is longer, as illustrated on the right.
The roads lie side-by-side, with a common starting point where each surveyor fixes one end of his tape measure.
Walking to the far end of the tarmac, they unroll their reels. As well as measuring their own stretch, the grafters both agree that their neighbour’s road is equal in length.
They estimate this by looking directly sideways from the end of their road, using a set square to accurately align the end of the other road with the correct point on their tape measure.
No disagreement so far. But what if one of the roads was rotated a bit?
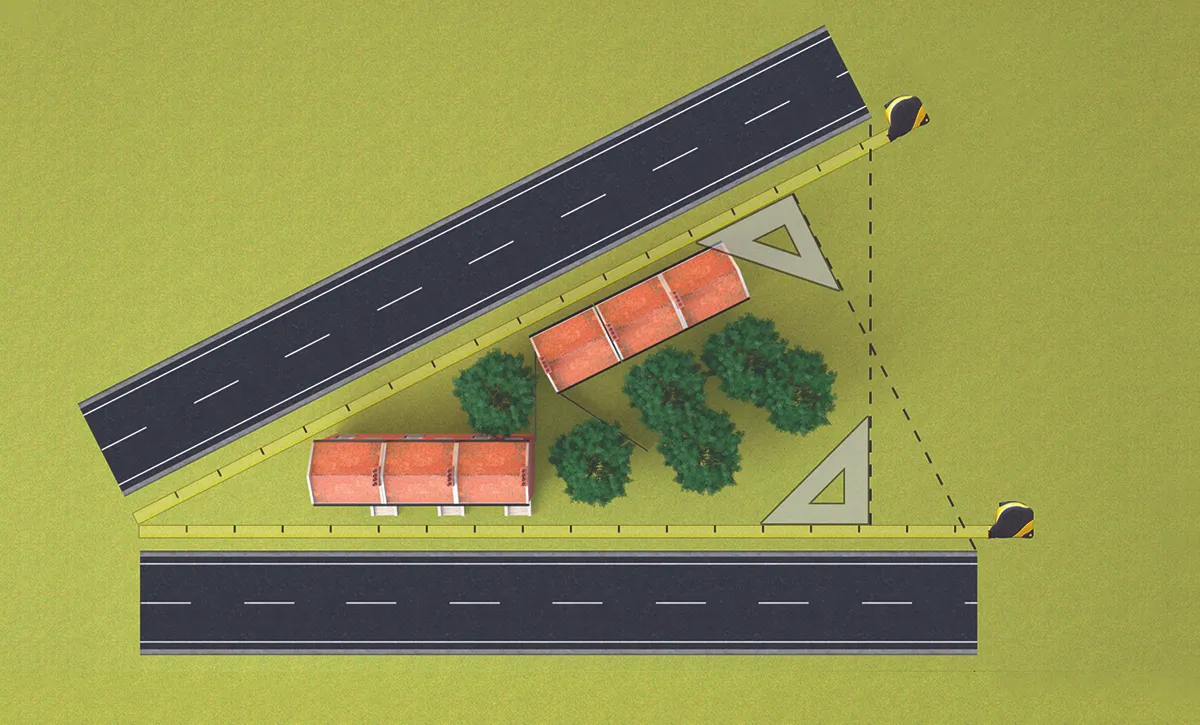
Each surveyor still measures their own road accurately but, because their tape and set square are no longer parallel to the other road, both judge that the other road is shorter than their own.
The second road doesn’t extend so far in the direction of the first tape measure and vice versa. In a similar way, returning to the twin paradox, Castor has lived for longer than Pollux in his own time direction, but Pollux has lived longer in the direction of his time.
There is an almost exact analogy between the lengths of the surveyors’ roads and the length of time between the twins’ clock ticks.
The only difference is that, as a road becomes rotated away from your measuring direction, its apparent length reduces, whereas a clock that is sent into a different spacetime direction (by moving fast) increases the time between its ticks.
This small difference in the ways that time and length coordinates mix together, within spacetime, ultimately makes us experience time and space in comfortingly different ways.
So it is ludicrous, after all, to say that my son is 10 miles old and a fortnight tall.
Yet it is not ludicrous to believe in time slowing down – a phenomenon that has helped us map high-energy cosmic rays.
And it is even rational to believe in a pair of twins who are each younger than the other. There is no paradox, because spacetime is real.
Space in 3D
What does it really mean to say that normal space is three-dimensional?
Three measurements are needed to locate an object in space. But it would take about a million measurements to reproduce a scale model of your house.
Does this mean that your house is one-million-dimensional? Of course not.
The three coordinates of a point in space are not separate measurements of three independent lengths.
Rather, they are three measurements with a special connection, and we can see that they are all connected by noticing that they can be mixed together.
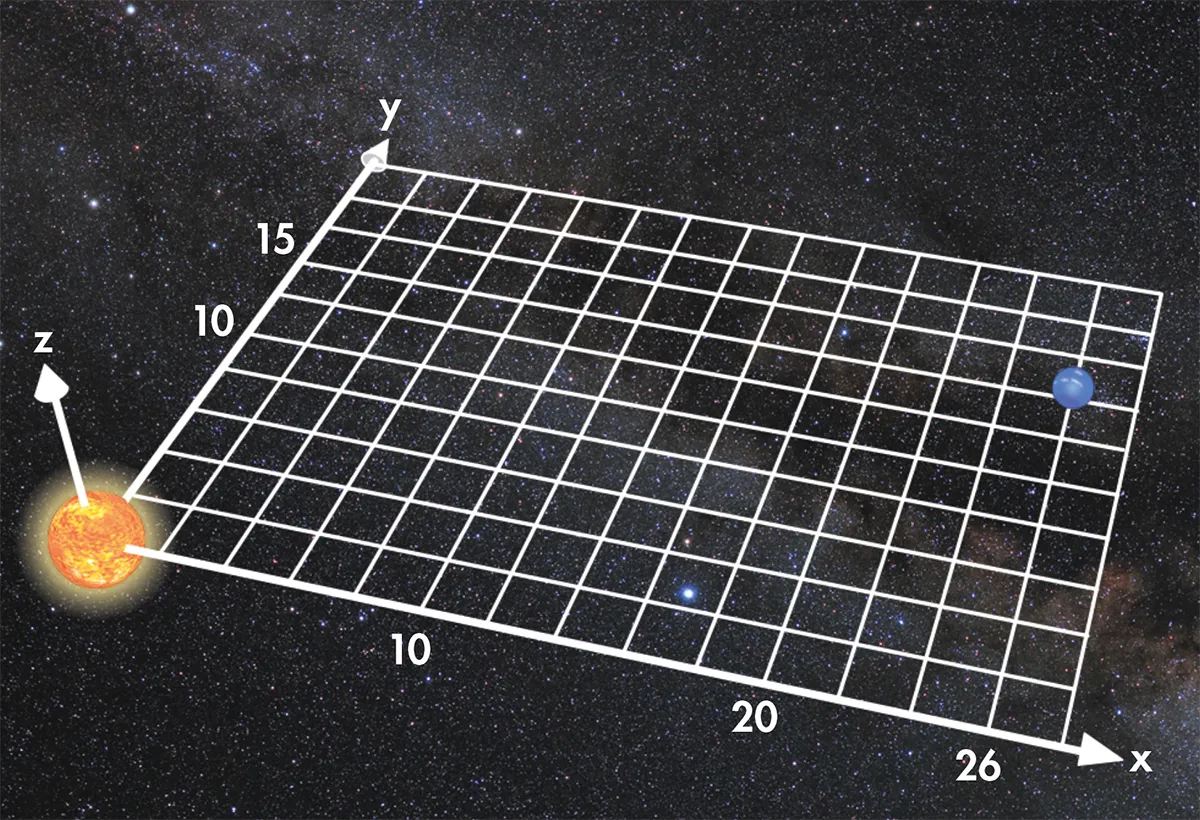
Our illustrations show the positions of the Sun, which is at the centre of the x, y and z axes, and Neptune. All of the axes are measured in astronomical units (AU).
In the illustration above, Neptune is 26 AU along the x direction, 15 AU along the y direction, and 0 AU (and therefore level with the Sun) in the z direction.
Its coordinates (x, y, z) are 26, 15, 0. But these three numbers depend on which arbitrary direction I chose to draw the coordinate axes.

Perhaps you also decided to measure Neptune’s coordinates, but you happened to draw your axes in a different arbitrary orientation, as in the illustration above.
You find that the planet lies 30 AU along your x direction, and is level with the Sun in your y and z directions. So, according to your rotated coordinate system, Neptune is at 30, 0, 0.
We both agree that Neptune, or any other object in space, needs three coordinates to locate it. But different observers can disagree about their values, because the numbers can get mixed up with each other by rotation.
